Інфіксне, префіксние і постфіксні вираження - Problem Solving with Algorithms and Data Structures

1. Перетворення інфіксне вираження в префіксних і Постфіксний
2. Узагальнене перетворення з інфіксне в постфіксний вид
3. постфіксні обчислення

Коли ви записуєте арифметичне вираз на кшталт B * C, то його форма надає вам достатньо інформації для коректної інтерпретації. В даному випадку ми знаємо, що змінна B множиться на змінну C, оскільки оператор множення * знаходиться в вираженні між ними. Такий тип запису називається інфіксной, оскільки оператор розташований між (in between) двох операндів, з якими він працює.

Розглянемо інший інфіксне приклад: A + B * C. Оператори + і * як і раніше розташовуються між операндами, але тут вже є проблема. З якими саме операндами вони будуть працювати? + Працює з A і B або * приймає B і C? Вираз виглядає неоднозначно.

Фактично, ви можете читати і писати вирази такого типу довгий час, і вони не будуть викликати у вас питань. Причина в тому, що ви дещо знаєте про + і *. Кожен оператор має свій пріоритет. Оператори з високим пріоритетом використовуються перш операторів з низьким. Єдиною річчю, яка може змінити порядок пріоритетів, є дужки. Для арифметичних операцій множення і ділення стоять вище додавання і віднімання. Якщо з'являються два оператора однакового пріоритету, то використовуються порядок зліва направо, або їх асоціативність.

Давайте інтерпретуємо викликало утруднення вираження A + B * C, використовуючи пріоритет операторів. B і C перемножуються першими, потім до результату додається A. (A + B) * C змусить виконати додавання A і B перед множенням. У вираженні A + B + C по черговості (через асоціативність) першим буде обчислюватися найлівіший +.

Хоча це очевидно для вас, пам'ятайте: комп'ютер потребує точному знанні того, як і в якій послідовності обчислюються оператори. Одним із способів записи вираження, що гарантує, що не виникне плутанини по відношенню до порядку операцій, є створення того, що називається виразом з повністю розставленими дужками. Такий тип виразу використовує пару дужок для кожного оператора. Дужки диктують порядок операцій, так що тут не виникає багатозначності. Так само відпадає необхідність пам'ятати правила розстановки пріоритетів.

Вираз A + B * C + D може бути переписано як ((A + (B * C)) + D) з метою показати, що множення відбувається в першу чергу, а потім слід крайнє ліве складання. A + B + C + D перепишеться в (((A + B) + C) + D), оскільки операції додавання асоціюються зліва направо.

Існує ще два дуже важливих формату виразів, які на перший погляд можуть здатися вам неочевидними. Розглянемо інфіксне запис A + B. Що станеться, якщо ми помістимо оператор перед двома операндами? Результуюче вираз буде + A B. Також ми можемо перемістити оператор в кінець, отримавши AB +. Все це виглядає дещо дивним.

Ці зміни позиції оператора по відношенню до операндам створюють два нових формату - префіксний і постфіксний. Префіксная запис вираження вимагає, щоб всі оператори передували двом операндам, з якими вони працюють. Постфіксний, в свою чергу, вимагає, щоб оператори йшли після відповідних операндів. Кілька додаткових прикладів допоможуть прояснити цей момент (див. таблицю 2 ).

A + B * C в префиксной нотації можна переписати як + A * B C. Оператор множення ставиться безпосередньо перед операндами B і C, вказуючи на пріоритет * над +. Потім слід оператор додавання перед A і результатом множення.

У постфіксной записи вираз виглядає як ABC * +. Порядок операцій знову зберігається, оскільки * знаходиться безпосередньо після B і C, позначаючи, що він має пріоритет вище наступного +. Хоча оператори переміщуються і тепер знаходяться до або після відповідних операндів, порядок останніх по відношенню один до одного залишається в точності таким, як був.

Таблиця 2: Приклади інфіксной, префиксной і постфіксной записиінфіксне записпрефіксних записПостфіксний запис

A + B + AB AB + A + B * C + A * BC ABC * +

А зараз розглянемо інфіксне вираз (A + B) * C. Нагадаємо, що в цьому випадку запис вимагає наявності дужок для вказівки виконати додавання перед множенням. Однак, коли A + B записується в префиксной формі, то оператор додавання просто поміщається перед операндами: + A B. Результат цієї операції є першим операндом для множення. Оператор множення переміщається в початок всього висловлювання, даючи нам * + AB C. Аналогічно, в постфіксной записи AB + явно вказується, що першим відбувається складання. Множення може бути виконано для отриманого результату і залишився операнда C. Відповідним Постфіксний виразом буде AB + C *.

Розглянемо ці три вирази ще раз (див. таблицю 3 ). Відбувається щось дуже важливе. Куди пішли дужки? Чому вони не потрібні нам в префиксной і постфіксной записи? Відповідь в тому, що оператори більше не є неоднозначними по відношенню до своїх операндам. Тільки інфіксне запис вимагає додаткових символів. Порядок операцій всередині префіксного і Постфіксний виразів повністю визначений позицією операторів і нічим іншим. Багато в чому саме це робить інфіксне запис найменш бажаною нотацією для використання.

Таблиця 3: Вираз з дужкамиінфіксне виразпрефіксних виразПостфіксний вираз

(A + B) * C * + ABC AB + C *

Таблиця 4 демонструє деякі додаткові приклади інфіксне виразів і еквівалентних їм префіксних і Постфіксний записів. Переконайтеся, що ви розумієте, чому вони еквівалентні з точки зору порядку виконання операцій.

A + B * C + D + + A * BCD ABC * + D + (A + B) * (C + D) * + AB + CD AB + CD + * A * B + C * D + * AB * CD AB * CD * + A + B + C + D + + + ABCD AB + C + D +

Перетворення інфіксне вираження в префіксних і Постфіксний

До сих пір ми використовували спеціальні методи для перетворення між інфіксне виразами і еквівалентними їм префиксной і постфікской записами. Як ви можете очікувати, існують алгоритмічні способи виконання таких перетворень, що дозволяють коректно трансформувати будь-який вираз будь-якої складності.

Першою з розглянутих нами технік буде використання ідеї повної розстановки дужок у виразі, розглянутої нами раніше. Нагадаємо, що A + B * C можна записати як (A + (B * C)), щоб явно показати пріоритет множення перед складанням. Однак, при ближчому розгляді ви побачите, що кожна пара дужок також відзначає початок і кінець пари операндів з відповідним оператором по середині.

Погляньте на праву дужку в подвираженія (B * C) вище. Якщо ми пересунемо символ множення з його позиції і видалимо відповідну ліву дужку, отримавши BC *, то відбудеться конвертація підвираз в Постфіксний нотацію. Якщо оператор додавання теж пересунути до відповідної правої дужки і видалити пов'язану з ним ліву дужку, то результатом стане повністю Постфіксний вираз (див. рисунок 6 ).

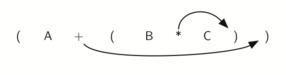
Малюнок 6: Переміщення операторів вправо для постфіксной записи

Якщо ми зробимо те ж саме, але замість пересування символу на позицію до правої дужки, зрушимо його до лівої, то отримаємо префіксних нотацію (див. рисунок 7 ). Позиція пари дужок насправді є ключем до остаточної позиції укладеного між ними оператора.

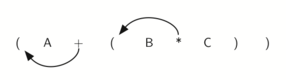
Малюнок 7: Переміщення операторів вліво для префиксной записи.

Таким чином, при перетворенні виразу (неважливо, наскільки складного) в префіксних або Постфіксний запис для встановлення порядку виконання операцій використовується повна розстановка дужок. Потім знаходиться всередині них оператор пересувається на крайню ліву або крайню праву позицію - залежно від того, префіксних або Постфіксний запис ви хочете отримати.

Ось більш складний вираз: (A + B) * C - (D - E) * (F + G). малюнок 8 демонструє його перетворення в постфіксний і префіксний види.

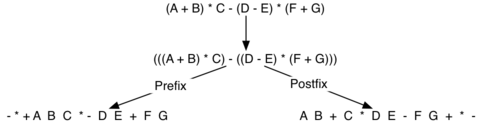
Малюнок 8: Перетворення складного виразу до префиксной і постфіксной записи.

Узагальнене перетворення з інфіксне в постфіксний вид

Нам необхідно розробити алгоритм перетворення будь-якого інфіксне вираження в Постфіксний. Для цього подивимося ближче на сам процес конвертації.

Розглянемо ще раз вираз A + B * C. Як було показано вище, його Постфіксний еквівалентом є ABC * +. Ми вже відзначали, що операнди A, B і C залишаються на своїх місцях, а місце розташування змінюють тільки оператори. Ще раз поглянемо на оператори в інфіксне вираженні. Першим при проході зліва направо нам попадеться +. Однак, в Постфіксний вираженні + знаходиться в кінці, так як наступний оператор, *, має пріоритет над складанням. Порядок операторів в первісному вираженні обернений результуючому Постфіксний висловом.

В процесі обробки вираження оператори повинні десь зберігатися, поки не знайдений їх відповідний правий операнд. Також порядок цих зберігаються операторів може бути зворотним (через їх пріоритету), як в даному прикладі зі складанням і множенням. Оскільки оператор додавання, що з'являється перед оператором множення, має більш низький пріоритет, то він повинен з'явитися після використання останнього. Через такого зворотного порядку має сенс розглянути використання стека для зберігання операторів до тих пір, поки вони не знадобляться.

Що щодо (A + B) * C? Нагадаємо його постфіксний еквівалент: AB + C *. Повторимося, що обробляючи це інфіксне вираз зліва направо, першим ми зустрінемо +. У цьому випадку, коли ми побачимо *, + вже буде поміщений в результуюче вираз, оскільки має перевагу над * в силу використання дужок. Тепер можна приступити до розгляду роботи алгоритму перетворення. Коли ми бачимо ліву дужку, то зберігаємо її як знак, що повинен буде з'явитися інший оператор з високим пріоритетом. Він чекатиме, поки не з'явиться відповідна права дужка, щоб відзначити його місце розташування (згадайте техніку повної розстановки дужок). Після появи правої дужки оператор виштовхується з стека.

Оскільки ми скануємо інфіксне вираз зліва направо, то для зберігання операторів будемо використовувати стек. Це надасть нам зворотний порядок, який був відзначений в першому прикладі. На вершині стека завжди буде останній збережений оператор. Коли б ми не прочитали новий оператор, ми повинні порівняти його з пріоритету з операторами в стеці (якщо такі є).

Припустимо, що інфіксне вираз є рядок токенів, розділених пробілами. Токенами операторів є *, /, + і - разом з правої і лівої дужками, (і). Токени операндів - це однобуквені ідентифікатори A, B, C і так далі. Наступна послідовність кроків дасть рядок токенів в Постфіксний порядку.

1. Створити порожній стек з назвою opstack для зберігання операторів. Створити порожній список для виведення.
2. Перетворити інфіксне рядок до списку, використовуючи строковий метод split.
3. Сканувати список токенов зліва направо.
   • Якщо токен є операндом, то додати його в кінець вихідного списку.
   • Якщо токен є лівою дужкою, покласти його в opstack.
   • Якщо токен є правою дужкою, то виштовхувати елементи з opstack поки не буде знайдена відповідна ліва дужка. Кожен оператор додавати в кінець вихідного списку.
   • Якщо токен є оператором *, /, + або -, помістити його в opstack. Однак, перед цим виштовхнути будь-який з операторів, які вже перебувають в opstack, якщо він має більший або рівний пріоритет, і додати його в результуючий список.

#. Коли вхідний вираз буде повністю оброблено, перевірити opstack. Будь-які оператори, все ще знаходяться в ньому, слід виштовхнути і додати в кінець підсумкового списку.

малюнок 9 демонструє алгоритм перетворення, що працює над виразом A * B + C * D. Зауважте, що перший оператор * видаляється до того, як ми зустрічаємо оператор +. Також + залишається в стеці, коли з'являється другий *, оскільки множення має пріоритет перед складанням. В кінці інфіксне вирази з стека двічі відбувається виштовхування, видаляючи обидва оператори і поміщаючи + як останній елемент в результуючий Постфіксний вираз.

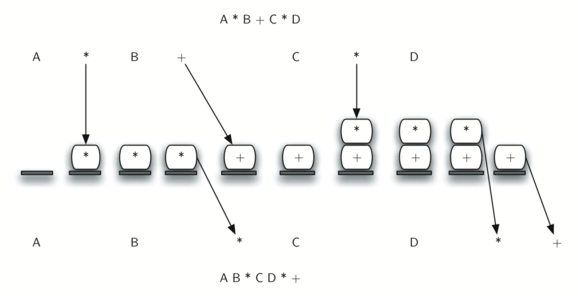
Малюнок 9: Перетворення A * B + C * D в Постфіксний запис

Щоб закодувати алгоритм на Python, ми будемо використовувати словник під ім'ям prec для зберігання значень пріоритету операторів. Він пов'язує кожен оператор з цілим числом, які можна порівнювати з числами інших операторів, як рівень пріоритетності (для цього ми довільно вибрали цілі числа 3, 2 і 1). Ліва дужка отримає найнижче значення. Таким чином, будь-який порівнюваний з нею оператор матиме пріоритет вище і розташовуватися над нею. Рядок 15 визначає, що операнди можуть бути будь-якими символами у верхньому регістрі або цифрами. Повна функція перетворення показана в ActiveCode 8 .

Run Save Load Show in Codelens

Перетворення інфіксне вираження в Постфіксний (intopost)

Нижче показані ще кілька прикладів виконання цієї функції.

>>> infixtopostfix ( "(A + B) * (C + D)") 'AB + CD + *' >>> infixtopostfix ( "(A + B) * C") 'AB + C *' >>> infixtopostfix ( "A + B * C") 'ABC * +' >>>

постфіксні обчислення

В останньому прикладі використання стека ми розглянемо обчислення виразу, яке вже знаходиться в постфіксной формі. В цьому випадку структурою для вирішення завдання знову обраний стек. Однак, оскільки ви скануєте Постфіксний вираз, чекати своєї черги повинні вже операнди, а не оператори, на противагу алгоритму вище. Ще один спосіб думати про це рішення: коли на вході виявиться оператор, для обчислення будуть використані два останніх операнда.

Щоб розібратися в цьому більш детально, розглянемо Постфіксний вираз 4 5 6 * +. Скануючи його зліва направо, ви перш за все натрапите на операнди 4 і 5. Що з ними робити невідомо, поки не відомий наступний символ. Приміщення кожного з них в стек гарантує їх доступність на випадок, якщо в такий з'явиться оператор.

У нашому випадку наступний символ - ще один операнд. Так що ми, як і раніше, поміщаємо його в стек і перевіряємо наступний символ. Бачимо оператор *, що означає множення двох останніх операндів. Зробивши виштовхування з стека двічі, отримаємо необхідні множники, а потім виконаємо множення (в даному випадку результатом буде 30).

Тепер можна обробити отримане значення, помістивши його назад в стек, щоб воно могло використовуватися в якості операнда для наступних операторів в вираженні. Коли буде оброблений останній оператор, в стеку залишиться тільки одне значення. Виштовхуємо його і повертаємо як результат вираження. малюнок 10 демонструє зміст стека протягом усього процесу обчислення виразу з прикладу.

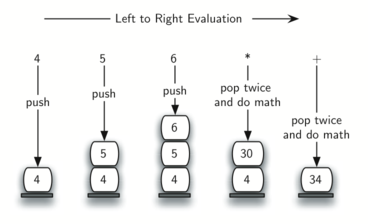
Малюнок 10: Зміст стека в процесі обчислення

на малюнку 11 показаний дещо складніший приклад: 7 8 + 3 2 + /. Тут є два моменти, які варто відзначити. Перший: розмір стека зростає, зменшується і знову росте в процесі обчислення подвираженій. Другий: обробляти оператор ділення потрібно дуже уважно. Нагадаємо, що операнди в Постфіксний вираженні йдуть в їх початковому порядку, оскільки постфікси змінює тільки положення оператора. Коли операнди поділу виштовхуються з стека, вони знаходяться в зворотній послідовності. Оскільки поділ не комутативними оператор (іншими словами, \ (15/5 \) не те ж саме, що \ (5/15 \)), ми повинні бути впевнені, що порядок операндів не змінився.

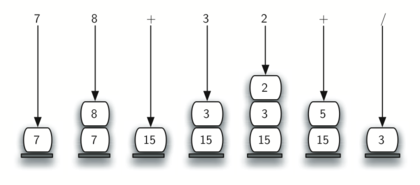
Малюнок 11: Більш складний приклад обчислення

Припустимо, що Постфіксний вираз - це рядок токенів, розділених пробілами. Операторами є *, /, + і -, а під операндами розуміються однорозрядні цілі значення. На виході буде цілочисельний результат.

1. Створюємо порожній стек під назвою operandStack.
2. Перетворюємо рядок до списку, використовуючи строковий метод split.
3. Скануємо список токенов зліва направо.
   • Якщо токен є операндом, то перетворюємо його з рядка в ціле число і поміщаємо значення в operandStack.
   • Якщо токен є оператором *, /, + або -, то він потребує двох операндах. Виробляємо виштовхування з operandStack двічі. Спочатку виштовхне другий операнд, а потім - перший. Виконуємо арифметичну операцію і поміщаємо результат назад в operandStack.
4. Коли вхідний вираз повністю оброблено, його результат знаходиться в стеку. Виштовхуємо його з operandStack і повертаємо в якості відповіді.

Повністю функція для обчислення Постфіксний виразів показана в ActiveCode 9 . Для допомоги з арифметикою визначена допоміжна функція doMath. Вона приймає два операнда і оператор, після чого здійснює належну арифметичну операцію.

Run Save Load Show in Codelens

Постфіксний обчислення (postfixeval)

Важливо відзначити, що для обох програм - Постфіксний перетворення і Постфіксний обчислення - ми припускаємо відсутність помилок у вхідному виразі. Використовуючи ці програми, як точку відліку, ви можете легко побачити, як в них можуть бути включені визначення помилок і повідомлення про це. Ми залишаємо це як вправу в кінці розділу.

самоперевірка

Q-45: Без використання функції activecode infixToPostfix перетворіть такий вираз в Постфіксний форму 10 + 3 * 5 / (16 - 4) Check Me Compare Me
Q-46: 17 10 + 3 * 9 / == Check Me Compare Me
Q-47: Модифікуйте функцію infixToPostfix таким чином, щоб вона могла конвертувати такий вираз: 5 * 3 ^ (4 - 2) Вставте відповідь сюди: Check Me Compare Me