Рівномірний прямолінійний рух

1. Визначення рівномірного прямолінійного руху визначення Рух матеріальної точки називають прямолінійним,...
2. Приклади завдань з рішенням

Визначення рівномірного прямолінійного руху

визначення

Рух матеріальної точки називають прямолінійним, якщо щодо обраної системи відліку траєкторією переміщення точки є пряма лінія.

Рух матеріальної точки вважають рівномірним, якщо за рівні проміжки часу точка здійснює рівні переміщення.

Припустимо, що точка рухається прямолінійно і рівномірно по осі X. Тоді координата ($ x $) точки є лінійною функцією часу:

\ [X = x_0 + vt \ left (1 \ right), \]

де $ x_0 $ - початкова координата точки, відповідна початку спостереження ($ x = x_0 (t = 0) $); $ V $ - швидкість руху точки.

Швидкість при рівномірному прямолінійному русі дорівнює відношенню зміни координати точки ($ \ Delta x = x-x_0 $) до проміжку часу ($ \ Delta t $) зміни цієї координати:

\ [V = \ frac {\ Delta x} {\ Delta t} \ left (2 \ right). \]

Рівномірний і прямолінійний рух характеризується постійністю вектора швидкості. Це означає, що швидкість руху точки не змінюється ні за модулем, ні за спрямуванням:

\ [\ Overline {v} = const \ \ left (3 \ right). \]

При прямолінійному русі шлях ($ s $) дорівнює за величиною зміни координати:

\ [S = \ left | x-x_0 \ right | \ left (4 \ right). \]

Зі швидкістю шлях прямолінійного руху пов'язаний як:

\ [S = vt \ \ left (5 \ right). \]

Графічний спосіб опису рівномірного прямолінійного руху

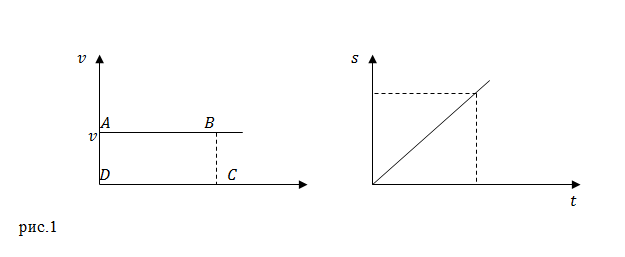
Найбільш наочним способом опису руху є графічний спосіб. Графік модуля швидкості при прямолінійній русі зображує рис.1. Це пряма паралельна осі часу, так як ми знаємо, що величина швидкості при рівномірному русі не змінюється. Площа прямокутника ABCD дорівнює за величиною зміни координати рухається точки за час її руху.

При рівномірному прямолінійному русі шлях прямо пропорційний часу руху (5). Значить, графіком відображає залежність шляху від часу є пряма, яка виходить з початку координат (рис.2) при $ s_0 \ left (0 \ right) = 0. \ $ Слід мати на увазі, що шлях не може бути менше нуля і не може зменшуватися при русі. Для визначення шляху, яке пройшла точка за встановлений проміжок часу випливає з точки на осі $ t $, яка відповідає кінця розглянутого часового проміжку, провести перпендикуляр до точки перетину з графіком, за тим відновити перпендикуляр з отриманої на графіку точки, на вісь s.

При рівномірному прямолінійному русі координата - це лінійна функція часу (1), отже, графік зміни координати від часу - це пряма (рис.3).

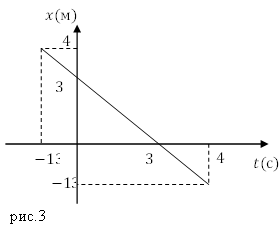
З графіка на рис.3 ми бачимо, що в початковий момент часу координата точки дорівнює $ x_0 \ left (t = 0 \ right) = $ 3м. У момент часу, що дорівнює трьом секундам координата точки дорівнює $ x_1 \ left (t = 3 \ right) = 0 \ м $ - це означає, що тіло, в момент часу дорівнює трьом секундам від початку спостереження, знаходилося на початку координат. У момент часу, рівний чотирьом секундам, точка знаходилося на осі X в точці з координатою $ x_2 \ left (t = 4 \ right) = - 1 \ м. \ $ Весь час свого руху точка переміщалася проти осі X. Швидкість точки протягом всього її руху дорівнює:

\ [V = \ frac {-1-3} {4} = - 1 \ \ left (\ frac {м} {з} \ right). \]

Знак мінус показує, що швидкість спрямована проти напрямку осі X, модуль швидкості дорівнює трьом метрам в секунду. За графіком залежності координати від часу можна знайти положення точки до початку спостереження, якщо рух частки не змінювалося. Моменти часу до початку спостережень вважають негативними. Так, судячи з графіку рис. 3 за одну секунду до початку спостережень координата точки дорівнювала 4 метрам.

Нагадаємо, що для побудови графіків, що описують прямолінійний і рівномірний рух досить знати координати (або значення шляху) для двох моментів часу.

Приклади завдань з рішенням

приклад 1

Завдання. Рух матеріальної точки задано двома графіками шляху від часу рис.4. Який з графіків відповідає більшій швидкості руху тіла?

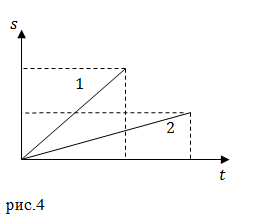
Рішення. Прямолінійний рух аналітично описує функція:

\ [S = vt \ \ left (1.1 \ right), \]

де $ v $ = const. Чим більше модуль швидкості, тим більший кут утворює графік $ s \ left (t \ right) $ з віссю часу. Отже, для графіка 1 величина швидкості руху більше.

Відповідь. $ v_2

приклад 2

Завдання. Матеріальна точка рухається рівномірно і прямолінійно проти осі Y. Швидкість руху дорівнює $ v = 1 \ \ frac {м} {з} $. Яким буде положення точки в момент часу рівний $ t = 20 $ c після початку відліку часу, якщо початкова координата частинки $ y_0 = 15 \ $ м? Який шлях, пройдений точкою?

Рішення. 1) При русі вздовж осі Y з постійною швидкістю рівняння для координати точки запишемо у вигляді:

\ [Y = y_0-vt \ \ left (2.1 \ right), \]

де знак мінус означає, що точка рухається проти осі Y. З умови задачі ми знаємо, що $ y_0 = 15 \ $ м, $ v = 1 \ \ frac {м} {з} $, $ t = 20 $ c підставимо задані величини, обчислимо координату:

\ [Y = 15-1 \ cdot 20 = -5 \ \ left (м \ right). \]

2) При рівномірному прямолінійному русі шлях, пройдений тілом, обчислюється як:

\ [S = vt = 1 \ cdot 20 = 20 \ (м) \]

Відповідь. $ Y = -5 \ м $, $ s $ = 20 м

Читати далі: рівноприскореного руху .